

 Return to Murrey Math
Return to Murrey Math
 Murrey Math Reversal Percentage Moves
Murrey Math Reversal Percentage Moves
Price Percentage Moves for Indexes over 500 but under 1000. (Intraday Basis) (Slow Day). One of the entries is this listing is: 6/8 ths 85% of the time 1.4648
((((1000/8) /8) /8) /8) = 1000/4096 = 0.244140625

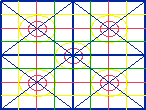
 Fractals
Fractals
----------------------------------------------------------------
| | | | |
| | | | |
|-------|-------| | |
| | | | |
| | | | |
|---------------|----------------| |
| | | |
| | | |
| | | |
| | | |
| | | |
|--------------------------------|-------------------------------|
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
----------------------------------------------------------------
FIGURE 1

 Fractional Brownian Motion
Fractional Brownian MotionEQ 1: < (X(t2) - X(t1)) ^ 2 > = k*((t2 - t1) ^ (2*H))
A B C D
1 X(9:33) X(10:21) COL_B - COL_A COL_C ^2
2 X(9:34) X(10:22) COL_B - COL_A COL_C ^2
3 X(9:35) X(10:23) COL_B - COL_A COL_C ^2
.
.
.
R X(2:21) X(3:09) COL_B - COL_A COL_C ^2
So < (X(t2) - X(t1)) ^ 2 > would be the sum of all the numbers in Column D divided by the number of samples (R). Where COL_A, COL_B, and COL_C denote the numbers in Column A, Column B, and Column C respectively.

 Statistical Nature of Price Changes
Statistical Nature of Price Changes| X(t2) - X(t1) |
Where the | | symbol means to take the absolute value of the number inside the vertical brackets. This just means that if X(t2) - X(t1) happens to be a negative number, then ignore the minus sign. Treat the number as if it was positive.
| P(X12) *
| *|||||*
| *|||||||*
| *|||||||||*
| *|||||||||||*
| *|||||||||||||*
| *|||||||||||||||*
| *|||||||||||||||||*
| *|||||||||||||||||||*
| *|||||||||||||||||||||*
| *|||||||||||||||||||||||*
| *|||||||||||||||||||||||||||*
| * ||||||||||||||||||||||||||||| *
| * ||||||||||||||||||||||||||||| *
| * ||||||||||||||||||||||||||||| *
|* ||||||||||||||||||||||||||||| *
-----------------------------------------------------------------
-z * S +z * S X12
FIGURE 2A
| P(X12) *
| * *
| * *
| * *
| * *
| * *
| * *
| * *
| * *
| * *
| * *
| * *
| * *
| * *
| * *
|*|||||| ||||||*
-----------------------------------------------------------------
-z * S +z * S X12
FIGURE 2B
X12 = X(t2) - X(t1)
1.0 - Shaded Area = Unshaded Area
(S ^ 2) = < (X(t2) - X(t1)) ^ 2 > = k*((t2 - t1) ^ (2*H))
EQ 1: < (X(t2) - X(t1)) ^ 2 > = k*((t2 - t1) ^ (2*H))
Assumptions 1 and 2 are pretty good assumptions. Together, these two assumptions make up the random walk model of markets (When H = 1/2). Some have questioned whether or not (X(t2) - X(t1)) is normally distributed. In general, however, the normal distribution is considered to be a good approximation.
This assumption is the basis of Murrey Math. Rejecting this assumption would require the rejection of Murrey Math.
This is a big assumption, but an argument may be made in favor of it. The Square in Time is a fractal. The rules for changing the scale of this fractal are to simply multiply the height and width of the square by 2 or by 1/2. This is a linear scaling. This can only be valid if H = 1.0. H relates the typical change in price < (X(t2) - X(t1)) > to the time interval (t2 - t1) i.e.
< (X(t2) - X(t1)) > is proportional to ((t2 - t1) ^ H)
The same statistical properties should be observed in a larger Square in Time as well as in a smaller Square in Time. This is the statistical self similarity property of price-time behavior. If we wished to consider price action over a longer time frame then we would multiply the time interval by 2.0 (this is how we scale the fractal). Lets do that:
((2 * (t2 - t1)) ^ H) = (2 ^ H) * ((t2 - t1) ^ H)
Note the term (2 ^ H). This term shows that if the time interval is doubled, then one would have to multiply the price range by (2 ^ H). If the scaling rule of the Square in Time is valid then H must be 1.0. Otherwise, we could not simply double price and double time when scaling the Square in Time.
I have no argument for this assumption other than convenience and wishful thinking. One has to start somewhere. This assumption may be valid based upon the way the Square in Time is defined. There may be a theoretical observation that could be used to prove k = 1.0 as was done for assumption (4) showing that H = 1.0. Algorithms are available for identifying the value of k. This would, however, require some computer programming that I do not have the time to perform currently. So, for now, k = 1.0.
(S ^ 2) = < (X(t2) - X(t1)) ^ 2 > = k*((t2 - t1) ^ (2*H))
Setting H = 1.0 and k = 1.0 yields:
(S ^ 2) = < (X(t2) - X(t1)) ^ 2 > = ((t2 - t1) ^ 2)
or
S = t2 - t1
with changes in X and t (price and time) expressed in units of
1/8'ths. Let's represent a change in X (price) using M/8 and let's
represent a change in t (time) using N/8,
where
M = 1, 2, 3, 4, 5, 6, 7, or 8
N = 1, 2, 3, 4, 5, 6, 7, or 8
z = (M/8)/(N/8) = M/N
PRICE
M ^
|
8 | .999 .999 .992 .954 .890 .816 .746 .683
|
7 | .999 .999 .980 .920 .838 .757 .683 .621
|
6 | .999 .997 .954 .866 .770 .683 .610 .547
|
5 | .999 .988 .905 .789 .683 .593 .522 .471
|
4 | .999 .954 .816 .683 .576 .497 .431 .383
|
3 | .997 .866 .683 .547 .451 .383 .332 .296
|
2 | .954 .683 .497 .383 .311 .259 .228 .197
|
1 | .683 .383 .259 .197 .159 .135 .111 .103
-------------------------------------------------------------->
N 1 2 3 4 5 6 7 8
TIME
TABLE 1
(A SQUARE OF 64)

 General Discussion
General Discussion
(change in price)/(change in time) = M/N

 Top of Page
Top of Page
 Return to Murrey Math
Return to Murrey Math Bonnie's Links
Bonnie's Links bonniehill@verizon.net
bonniehill@verizon.net last modified on February 9, 2020
last modified on February 9, 2020
URL: http://mysite.verizon.net/bonniehill/pages.aux/murrey/TKnotes.2.html
